今天，我們先來看一個數學題，所有正整數無窮相加，即1+2+3+4+5+……，它的值是多少呢？也許有觀眾朋友說，雖然我無法一下子給出答案，但是按照常理推，這個結果應該是一個非常大的數字。
不過呢，在數學界中一旦涉及到無窮，就和物理學進入量子力學一樣，一切都不能用正常思維去思考了。1+2+3一直加到無窮最後的結果竟然是-1/12。而給出這個公式證明的人，就是我們今天故事的主人公，被稱為從未來穿越而來的天才數學家拉馬努金（Srinivasa Ramanujan）。
拉馬努金為什麼算天才呢？因為他從小沒有受過正規的訓練，卻表現出了異於常人的數學天賦，僅憑「直覺」就能寫下極其複雜的數學公式。在他短暫的一生中，拉馬努金留下了將近4000個公式及命題，由於他沒給出證明過程，所以當時沒有人能看懂這些公式。在很多年之後，數學家們才解開了其中的一些公式命題，甚至由此獲得重大數學成就。比如，比利時數學家德利涅（V. Deligne）在1973年證明了拉馬努金1916年提出的一個猜想，並因此獲得了1978年的菲爾茲獎，而這是世界上最高的數學獎榮譽。
那為什麼又說拉馬努金是穿越而來的呢？因為當代科學家在研究他那些神祕的公式時，赫然發現，他寫下的好幾個定理涉及到粒子物理、統計力學、計算機科學、密碼技術和空間技術等不同領域。而1919年，在拉馬努金生命的最後一年，他寫出的最後一個公式，到2012年才被人破解，數學家表示這一函數可以用來描述黑洞的行為，要知道，當拉馬努金首次提出這種函數的時候，人們連黑洞是什麼都還不知道呢。
拉馬努金的伯樂、導師兼好友，英國大數學家哈代（G. H. Hardy）曾表示自己一生對數學領域最大的貢獻就是發掘了拉馬努金，他還感歎，「我們是在學習數學，而拉馬努金則是發現並創造了數學。」
而拉馬努金也不止一次地向哈代表示，甚至證實他的數學天賦來自於神，這一切也都深深震撼著持有無神論觀點的哈代。
天才出世
1887年12月12日，在印度埃羅德（Erode），一個遠離邦首府馬德拉斯（Madras）的小鎮，有一個男孩降生了，家人為他取名叫拉馬努金。埃羅德是一個很貧窮的小鎮，即便拉馬努金的家族屬於印度種姓制度中最高等級，他們家還是相當貧窮，全家人就靠父親每月的工資20盧比生活，日子過得緊巴巴的。
小拉馬努金並不像一些天才兒童，三四歲就展露頭角，他的才華直到1898年，他十歲的時候，才逐漸被發現。那一年，小拉馬努金進入了一所學校讀書，第一次接觸到正規的數學。而這時，他的家裡也住進了兩個房客，時不時也教小拉馬努金一些數學。等拉馬努金11歲時，這兩位房客已經感到自己的數學能力已經教不了這個孩子了，而這兩位房客也不是一般人，他們是當時政府大學的大學生。
拉馬努金12歲時，高班的同學借給他一本朗內（S. L. Loney）寫的《平面三角學》（Plane Trigonometry）。令人驚訝的是，拉馬努金在短時間裡自學完整本書，不僅解答出書中所有的問題，還獨立推導出歐拉公式（Euler’s formula）。
拉馬努金進入高中後，一次在學校圖書館中他借到了英國數學家G‧S‧卡爾（George Shoobridge Carr）的《純粹及應用數學的基本成果概要》（A Synopsis of Elementary Results in Pure and Applied Mathematics）一書。這是一本讓一般人頭大的數學著作，裡面包含著代數、微積分、三角學和解析幾何的5000多個公式，但沒有給出詳細證明。然而，拉馬努金卻愛不釋手，最後用自己的方式，把所有的公式都證明了一遍。
拉馬努金因為數學成績優異曾獲得獎學金，然而他偏科太嚴重，除了數學，他什麼也不感興趣。結果，到學期末他因為英語等成績太差而失去獎學金，並最終因為文科成績不合格而被迫輟學。
窮困潦倒中的磨礪
離開學校之後，拉馬努金繼續過著貧困的生活。1909年，他結婚了，按照傳統他必須得外出謀生養家了。拉馬努金找到印度數學學會的創始人之一艾亞爾（R. Aiyar），請他給自己一份餬口的差事。是金子總是會發光的。拉馬努金後來被推薦給印度數學學會的另一位創始人拉奧（R. Rao）。拉奧愛惜拉馬努金的才華，表示願意按時給拉馬努金一些錢，維持他一段時期的生活，同時向有關方面為拉馬努金爭取研究津貼，以使他能安心從事研究。
然而，孟子說過：「天將降大任於斯人也，必先苦其心志，勞其筋骨，餓其體膚，空乏其身。」拉奧為拉馬努金申請的津貼沒有拿下來，而拉馬努金也很有志氣，不願意成為別人的經濟包袱，也很長時間不去拉奧那裡領錢了。因為沒錢買紙，拉馬努金都是在石板上做數學演算，然後直接用胳膊肘去擦，時間一長，胳膊肘被磨得又黑又厚。
生活還得繼續啊，好在拉奧等人是真心願意幫助這個有才華的年輕人，他們幫拉馬努金在金奈（Chennai），原名叫馬德拉斯（Madras）的港務局找到一份工作，月薪25盧比。雖然薪水不多，但總是可以解決溫飽問題了。於是，拉馬努金把精力投入在數學研究中，並開始初步嶄露頭角。
他在著名的《印度數學會雜誌》（Journal of the Indian Mathematical Society）上發表了一些論文，在印度的數學圈漸漸有了名氣。因為當時英國的數學研究做得很好，於是有人就建議拉馬努金聯繫聯繫英國的數學家。
仔細思考之後，拉馬努金給英國劍橋大學的幾位著名數學家發了一份一模一樣的信。
大洋彼岸的神祕來信
1913年的一個冬日，英國劍橋大學三一學院的數學教授哈代在吃完早飯之後，按照慣例拿起桌邊的《泰晤士》報紙，準備了解當日新聞。這時，報紙上放著的一封信引起了他的注意。信封上貼著來自印度的郵票，並寫著「馬德拉斯，1913年1月16日」。雖然自己似乎在印度馬德拉斯沒有熟人，哈代還是打開了信封，抽出了長達10頁的信。
作為著名的數學家，哈代經常收到這類毛遂自薦的信，然而拉馬努金的信讓他頗為驚訝。整封信除了幾句英語介紹之後，完全就是用代數、三角函數、微積分這樣的數學語言寫成的。滿眼的公式啊，估計哈代都要看暈了。
當天晚上，哈代找來了他的好友，也是著名數學家李特爾伍德（J. E. Littlewood）一起研究這份信。從晚上9點到凌晨12點，三個小時過去了，他們倆竟然都沒有完全看懂信中的公式。但是有一件事他們已經清楚了，就是這個寫信的人一定是個數學天才。
哈代興奮地向拉馬努金發出邀請，並為他申請了豐厚的獎學金。然而，拉馬努金這邊卻遲疑了，因為他的家人擔心他一旦出國就會失去在印度的高貴種姓。直到有一天，拉馬努金的媽媽在睡夢中夢到神告訴她，不要阻擋兒子的前程，這樣她才下決心讓兒子出國。
天才的鼎盛時期
來到英國之後，拉馬努金在哈代和李特爾伍德等人的幫助下，學習了很多數學的基礎知識，以及正規的數學研究方法，在歐洲的5年裡，他在英國、法國、德國的數學雜誌上共發表了21篇論文。
在拉馬努金與哈代合寫的一篇論文中，他們對困擾數學家多年的整數分拆問題作出了驚人的解決，首創了正整數n的分拆數p(n)的漸近公式。
這裡稍微介紹下正整數拆分，就是對於一個正整數n，它可以有1個或多個正整數疊加而成，p(n)就代表了不同的疊加方式。
比如：1=1, p(1) =1
2=2, 2=1+1, p(2)=2
3=3, 3=1+1+1, 3=1+2, p(3)=3
4=4, 4=1+1+1+1, 4=1+1+2, 4=1+3, 4=2+2, p(4)=5
……..
我們這裡也展示下拉馬努金和哈代的公式：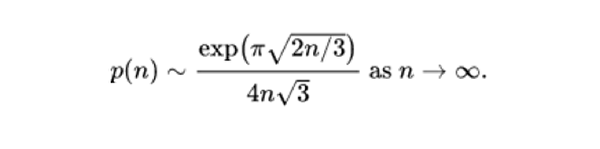
憑藉著這個公式，拉馬努金於1918年被推選為英國王家學會會員，這是英國數學界的最高榮譽，而拉馬努金也是有史以來最年輕的會員。
哈代對於拉馬努金的才華非常欣賞，他在自己設計的一種關於數學天才的非正式的評分表中，給自己評了25分，給好友兼數學家李特爾伍德評了30分，給他同時代最偉大的數學家希爾伯特（D. Hilbert）評了80分，而他給拉馬努金，評了100分。
他時常對拉馬努金寫的公式讚不絕口，問他：你是怎麼寫出來？而拉馬努金則常常簡單地回答道：這是神在夢中指點給我的。拉馬努金自己說，在睡夢中他的思路就會變得很清晰，能夠接受到海量信息。在夢中，神在牆上寫下一個又一個公式，他記住那些公式，醒來後，把公式記錄在筆記本上。
一開始，信仰無神論的哈代以為拉馬努金是在逗他玩呢，然而一次又一次，拉馬努金在睡醒覺之後，就給出了令他們頭疼的難題的答案，讓哈代著實吃驚不已。看著拉馬努金那三大本筆記本，上面寫滿了超級複雜又沒有證明過程的公式，哈代逐漸相信，拉馬努金確實有不同於常人的特殊能力，他或許真的能和神溝通。
哈代很高興自己發掘出了天才拉馬努金。然而，他們快樂的合作生活只維持了三年。
最後的時刻
拉馬努金如痴如醉地把一切精力投入到數學研究之中，經常忘記吃飯，忘記休息，他的身體時常出現疼痛，最後在1917年發現他患上了肺結核，他在英國的最後一年，幾乎都是在療養院度過的。然而，在病床上，拉馬努金還是在想著數學。
這裡還有一個小插曲。有一天，哈代乘坐一輛出租汽車去療養院看望拉馬努金。哈代對拉馬努金說：「我搭計程車來，車牌號碼是1729，這數字真沒趣，希望不是不祥之兆。」拉馬努金想一下馬上回答：「不，這個數有趣得很。在所有可以用兩個立方數之和來表達，而且有兩種表達方式的數之中，1729是最小的。」即1729=1^3+12^3=9^3+10^3，後來這類數稱為的士數。難怪，哈代會發出感歎：「每個數都是拉馬努金的朋友。」
久病沒有好轉的拉馬努金思鄉心切，在1919年回到印度，然而這並沒有讓他好起來，轉過年來的4月，拉馬努金病逝，當時他只有33歲。他一生清貧，死後僅留下兩張照片，以及一個熱敷用的熱水袋和一些書籍文稿。
拉馬努金在病床上，還留下了第四本記錄公式的筆記本，這本筆記本被稱為「遺失的筆記本」，因為在他死後50多年一直都不知下落。直到1976年，美國賓夕法尼亞大學教授G‧安德魯斯（G. Andrews）訪問劍橋大學三一學院時，在該校的圖書館中發現這本筆記本，上面有600多個沒有證明過程的公式。
當現代的科學家研究拉馬努金的這幾本手稿時，發現它們如同一個巨大的寶藏，蘊含著眾多難以揭開的奧祕。拉馬努金的一些公式在眾多尖端科學領域起著重要的作用，甚至隱藏著黑洞的祕密。
拉馬努金一生堅信，他的數學靈感來自於神，或許也只有這樣才能解釋，為何他能有如此超凡的成就。拉馬努金的故事，後來在2015年被拍成電影《知無涯者》。據說，數十位硅谷科技領袖在一次宴會中一起看了這部電影，很多人最後紅著眼眶走了出來。
好了，今天就和大家分享到這裡，未解之謎，我是扶搖，我們下期再見。
歡迎訂閱Youmaker頻道：https://www.youmaker.com/c/UnsolvedMystery
訂閱頻道YouTube頻道：https://www.youtube.com/channel/UCzvQZ1p_-AXgAWiyHhE7CxQ
訂閱未解之謎Telegram群組：https://t.me/wjzmchannel
【未解之謎】節目組製作
責任編輯：李梅#
